Conic sections are the curves obtained from intersecting a plane with a cone. These curves have a unique placement in mathematics and various applications in physics, engineering, and astronomy. The four primary conic sections are circles, ellipses, parabolas, and hyperbolas. This article will explore each conic section, providing detailed explanations, properties, and example problems with solutions for each.
Conic sections: Circles
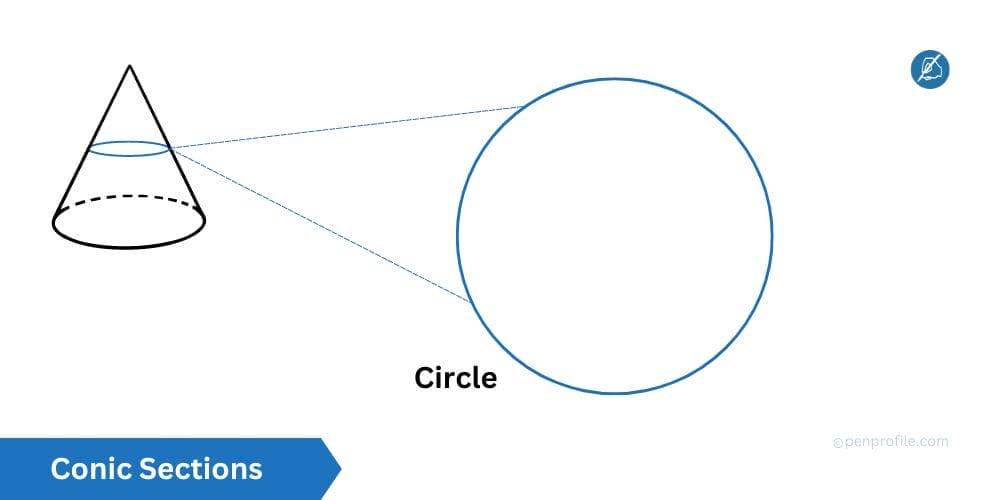
A circle is one of the fundamental shapes in geometry and is also a part of a conic section. It is the set of all points which are equidistant from the center which is always in a fixed point. The distance between any point on the circle to the center of the circle is known as the radius of the circle.
When it comes to mathematics, shapes are often expressed as equations and the circle is no different. Mathematically, the circle can be denoted by the standard equation \((x−h)^2+(y−k)^2=r^2\), where \((h,k)\) is the coordinate or location of the center, and the radius is denoted by r. The standard equation of a circle actually comes from the distance formula, ensuring that any point \((x, y)\) along the circle is exactly r unites away from the center \((h,k)\). Some properties of circles include, constant curvature, equal radii, and rotational symmetry about the center.
- Standard Equation: \((x – h)^2 + (y – k)^2 = r^2\)
- \((h, k)\) is the center.
- \(r\) is the radius.
Circle example problems and solutions
Problem 1
Given the equation of a circle \((x – 3)^2 + (y + 4)^2 = 25\), find the center and radius of the circle.
Solution:
- The equation \((x – 3)^2 + (y + 4)^2 = 25\) is in standard form.
- The center \((h, k)\) is \((3, -4)\).
- The radius \(r\) is \(\sqrt{25} = 5\).
Problem 2
Find the equation of a circle with center at \((2, -3)\) and passing through the point \((5, 1)\).
Solution:
- The radius \(r\) is the distance between \((2, -3)\) and \((5, 1)\).
- \(r = \sqrt{(5 – 2)^2 + (1 + 3)^2} = \sqrt{3^2 + 4^2} = \sqrt{9 + 16} = 5\).
- The equation of the circle is \((x – 2)^2 + (y + 3)^2 = 5^2\) or \((x – 2)^2 + (y + 3)^2 = 25\).
Conic sections: Ellipses
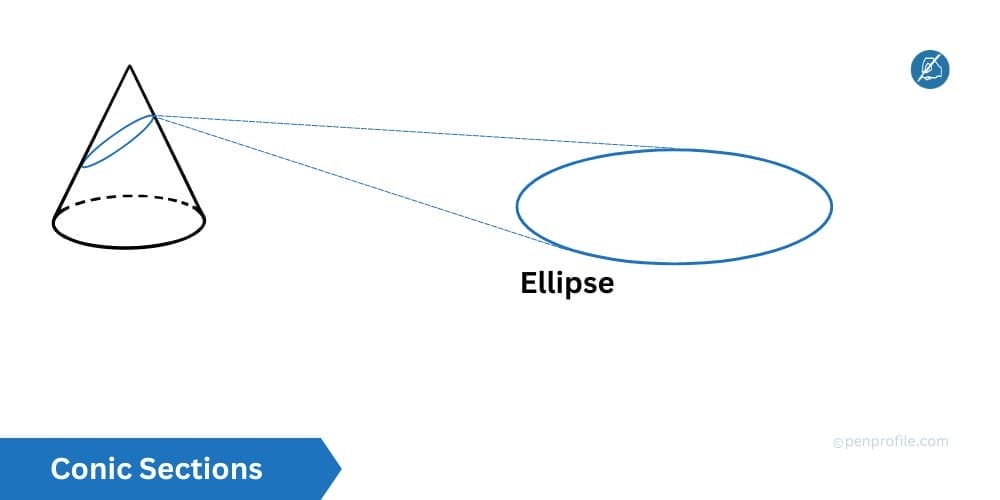
An ellipse is another conic section which is formed from intersecting a plane with a cone at a specific angle such that the plane is not intersecting the base of the cone. It is the set of all points in a plance upon where the sum of the distances from any two fixed points, also known as the foci, is constant.
An ellipse has a major and minor axis. The major axis is always the longest diameter that is passing through both foci. The minor axis is the shortest diameter which is perpendicular to the major axis at the center. Just like a circle, the ellipse also has an equation that defines it mathematically. The standard equation for an ellipse is given by \(\frac{(x – h)^2}{a^2} + \frac{(y – k)^2}{b^2} = 1\) for a horizontal ellipse and \(\frac{(x – h)^2}{b^2} + \frac{(y – k)^2}{a^2} = 1\) for a vertical ellipse, where \(h,k\) is the center, a is the semi-major axis, and b is the semi-minor axis.
- Standard Equation:
- Horizontal: \(\frac{(x – h)^2}{a^2} + \frac{(y – k)^2}{b^2} = 1\)
- Vertical: \(\frac{(x – h)^2}{b^2} + \frac{(y – k)^2}{a^2} = 1\)
- \((h, k)\) is the center.
- \(a\) is the semi-major axis.
- \(b\) is the semi-minor axis.
Ellipse example problems and solutions
Problem 1
Given the equation \(\frac{(x – 1)^2}{16} + \frac{(y + 2)^2}{9} = 1\), find the center, lengths of the major and minor axes.
Solution:
- The center \((h, k)\) is \((1, -2)\).
- \(a^2 = 16 \Rightarrow a = 4\), so the length of the major axis is \(2a = 8\).
- \(b^2 = 9 \Rightarrow b = 3\), so the length of the minor axis is \(2b = 6\).
Problem 2
Find the equation of an ellipse with center at \((0, 0)\), a semi-major axis of 5 along the x-axis, and a semi-minor axis of 3 along the y-axis.
Solution:
- Since the center is at \((0, 0)\) and the semi-major axis is along the x-axis, \(a = 5\) and \(b = 3\).
- The equation is \(\frac{x^2}{5^2} + \frac{y^2}{3^2} = 1\) or \(\frac{x^2}{25} + \frac{y^2}{9} = 1\).
Conic sections: Parabola
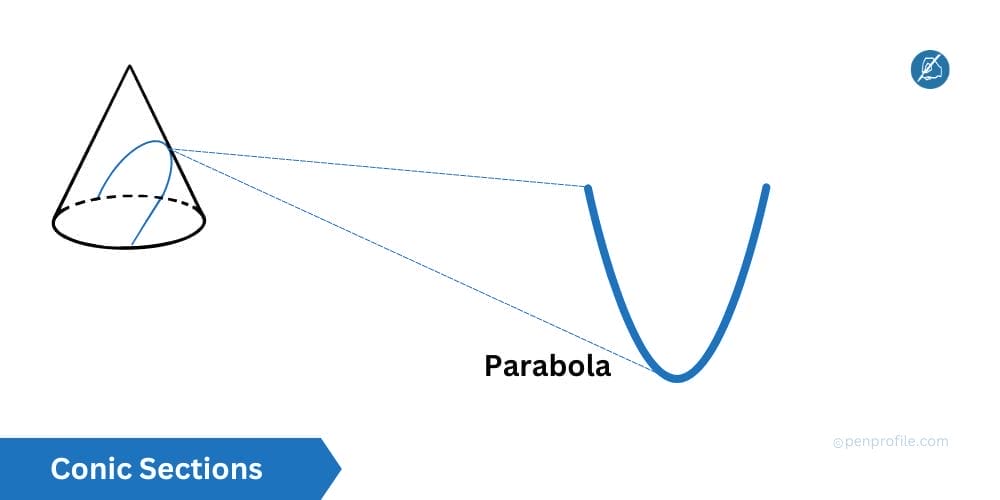
The next conic section parabola, is defined as the set of all points in a plane equidistant from a fixed point, called a focus, and a fixed line that is called the directrix. Parabolas have a distinct “U” shape which can open up in any direction, upward, downward, left, or right all depending on its orientation.
The standard equation for a parabola is \((x – h)^2 = 4p(y – k)\) for a vertical oriented parabola which opens up upward or downward and \((y – k)^2 = 4p(x – h)\) for a horizontal oriented parabola which opens up left or right. As before, \(h,k\) is the vertex and p is the distance from the vertex to the focus. The value of p is the thing that determines the width as well as steepness of the parabola. A parabola also has an axis of symmetry which is a line that passes directly at the center or vertex of the parabola providing a mirror image on either side.
- Standard Equations:
- Vertical: \((x – h)^2 = 4p(y – k)\)
- Horizontal: \((y – k)^2 = 4p(x – h)\)
- \((h, k)\) is the vertex.
- \(p\) is the distance from the vertex to the focus.
Parabola example problems and solutions
Problem 1
Given the equation \((x – 2)^2 = 12(y + 3)\), find the vertex, focus, and directrix of the parabola.
Solution:
- The equation is in the form \((x – h)^2 = 4p(y – k)\).
- The vertex \((h, k)\) is \((2, -3)\).
- \(4p = 12 \Rightarrow p = 3\).
- The focus is \((2, -3 + 3) = (2, 0)\).
- The directrix is \(y = -3 – 3 = -6\).
Problem 2
Find the equation of a parabola with vertex at \((0, 0)\) and focus at \((0, 4)\).
Solution:
- Since the focus is at \((0, 4)\), \(p = 4\) and the parabola opens upwards.
- The equation is \((x – 0)^2 = 4 \cdot 4 (y – 0)\) or \(x^2 = 16y\).
Conic sections: Hyperbola
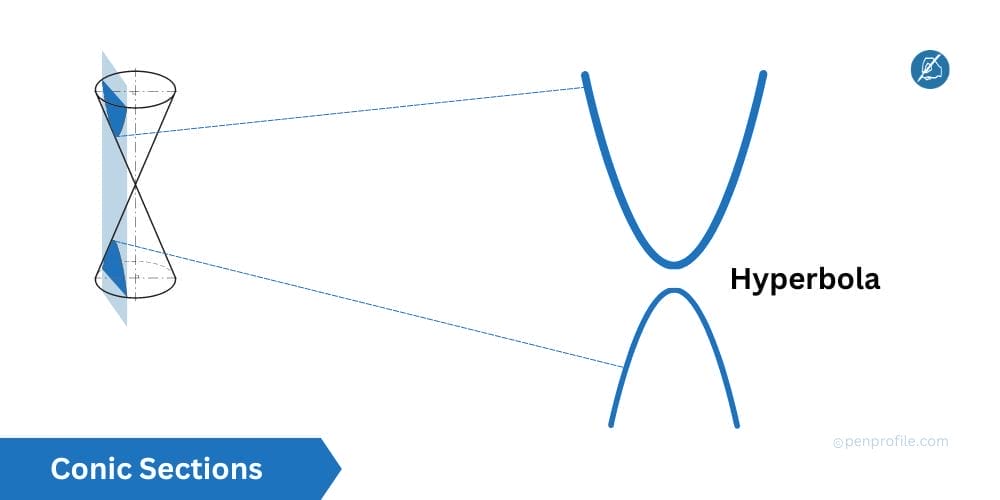
A hyperbola is unique kind of conic section in the sense that it requires two cones or double cones to form. A hyperbola is formed when a plane intersects both nappes of a double cone. Unlike an ellipse, which has a constant sum of distances from its foci, a hyperbola has aa constant difference of distances from its foci. This actually leads to the production of two separate mirror image curves called branches.
Hyperbolas also have two axes of symmetry known as the transverse axis and the conjugate axis. The transverse axis passes through the vertices whereas the conjugate axis which is perpendicular to the transverse axis is at the center. The standard equation for a hyperbola is \(\frac{(x – h)^2}{a^2} – \frac{(y – k)^2}{b^2} = 1\) for a horizontal hyperbola and \(\frac{(y – k)^2}{a^2} – \frac{(x – h)^2}{b^2} = 1\) for a vertical hyperbola. Where as always, \((h, k)\) is the center, a is the distance between the center and the vertices, and b is the distance between the center to the co-vertices.
- Standard Equations:
- Horizontal: \(\frac{(x – h)^2}{a^2} – \frac{(y – k)^2}{b^2} = 1\)
- Vertical: \(\frac{(y – k)^2}{a^2} – \frac{(x – h)^2}{b^2} = 1\)
- \((h, k)\) is the center.
- \(a\) and \(b\) relate to the distances from the center to the vertices and co-vertices, respectively.
Hyperbola example problems and solutions
Problem 1
Given the equation (\frac{(x – 1)^2}{9} – \frac{(y + 2)^2}{16} = 1), find the center, lengths of the transverse and conjugate axes.
Solution:
- The center \((h, k)\) is \((1, -2)\).
- \(a^2 = 9 \Rightarrow a = 3\), so the length of the transverse axis is \(2a = 6\).
- \(b^2 = 16 \Rightarrow b = 4\), so the length of the conjugate axis is \(2b = 8\).
Problem 2
Find the equation of a hyperbola with center at \((0, 0)\), vertices at \((\pm 5, 0)\), and foci at \((\pm 7, 0)\).
Solution:
- Since the vertices are at \((\pm 5, 0)\), \(a = 5\).
- The distance from the center to the foci is \(c = 7\).
- Using \(c^2 = a^2 + b^2\), \(7^2 = 5^2 + b^2\), \(49 = 25 + b^2\), \(b^2 = 24\), \(b = \sqrt{24}\).
- The equation is \(\frac{x^2}{25} – \frac{y^2}{24} = 1\).
Mastering conic sections requires understanding their definitions, properties, and standard equations. By solving various example problems, one can gain deeper insights into these fascinating curves. Each conic section, circle, ellipse, parabola, and hyperbola will offer unique properties and applications, making them essential topics in mathematics and related fields. Whether for academic purposes or practical applications, proficiency in conic sections enhances one’s mathematical toolkit.













