Trigonometry is a fundamental part of mathematics. This branch studies the right angle triangle and its calculations for angles and side lengths. It helps us find out the unknown sides and angles of a right angled triangle using trigonometric functions and formulas. This article will be diving into the most basic calculations for a right angled triangle; Pythagorean theorem and Sine, Cosine, and Tan functions.
Triangles
A triangle is a polygon with three sides and an interior angle sum of 180 degrees.
There are six types of triangles in mathematics and you can either identify them by its interior angle or by the length of the sides.
By its interior angles:
Acute triangle: A triangle with an angle that is less than 90 degrees.
Obtuse triangle: A triangle with an angle that is greater than 90 degrees.
Right angle triangle: A triangle with a 90 degree angle.
By its side:
Scalene triangle: A triangle with no equal side length.
Isosceles triangle: A triangle with 2 equal side lengths.
Equilateral triangle: A triangle with all 3 sides equal in length.

Right angled triangle
A right angled triangle is a triangle that has at least one of its interior angles as 90°.

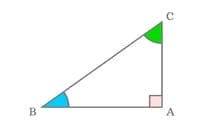
Properties of a right angle triangle:
- The side opposite angle of 90° is the hypotenuse.
- The hypotenuse is always the longest side.
- The sum of the other two interior angles is equal to 90°.
- The 90°angle is often indicated by a small square.
Pythagorean Theorem: the ultimate equation for side lengths
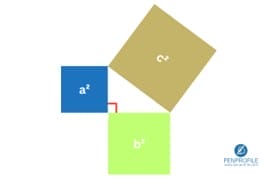
The Pythagorean Theorem is an important equation that everyone should have memorized because it’s the simplest and fastest way to find a missing or unknown side of a right angle triangle. In some cases, you can even use it to find an angle in the right angle triangle.
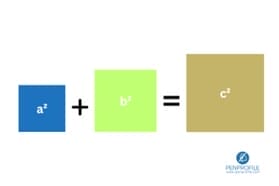
According to the Pythagorean Theorem, the sum of the areas of the two squares on the legs (a and b) equals the area of the square on the hypotenuse ( c).
$$
a^2+b^2=c^2
$$
c is the Hypotenuse (Hyp).
The hypotenuse is the side opposite to the angle that is 90°
a is Adjacent (Adj).
b is Opposite (Opp).
The adjacent and opposite (a and b) side is simply the other two legs of the triangle. So, it can be any side of your choice except in cases like the SOH CAH TOA formulas, the opposite would be the side opposite to the given angle and adjacent is the side next to it.
Solving questions
Following the examples below, you will see that we can solve questions of different types using the Pythagorean Theorem just by rearranging the \(a^2+b^2=c^2\) equation.
Question 1

The first step when solving a question using the Pythagorean Theorem equation is to identify whether or not the triangle before you is a right angle triangle.
The one above us is clearly a right angle triangle because of the little square on the inside that indicates a 90 degree angle.
Step 2: Identify which of a, b, and c are we trying to solve.
Because the side opposite to the 90° angle is called the hypotenuse and is the one missing a number, we are solving for c.
Step 3: Rearrange the equation.
While you can solve the question without rearranging anything, transforming your formula for the missing side to be the subject of the formula, makes solving it more straightforward.
To make c the subject of the formula you will need to remove the 2 in c by rooting the other side of the formula to become \(c=\sqrt{a^2+b^2}\).
Step 4: Substitution.
Substitute all the information given to you into the new formula to become \(c=\sqrt{9^2+10^2}\).
If you are using a calculator, by step 4 you’ve already gotten your answer.
Step 5: Solve step by step.
\(9^2=9×9=81\)
\(10^2=10×10=100\)
\(81+100=\sqrt{181}\)
Hypotenuse (x) is 13.45
Question 2
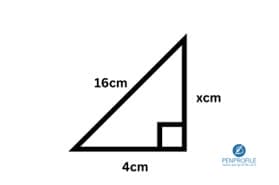
If you understood question 1, you’ll now be able to solve the next questions, as the steps are identical. Except in the rearranging step, which we’ll see how and why it differs right now.
Step 1: identify the type of triangle.
Answer: right angled triangle.
Step 2: Identify a, b, and c.
c=16cm. Let’s take a as 4cm and b will be our missing length.
Step 3: rearrange the equation.
We need to make b the subject of the formula for this question so, first we need to move +c² to the other side of the equation while +b² will replace c².
\(c^2-a^2=b^2\). Note that instead of addition the equation has turned to subtraction now because we moved the places of the variables and so their signs changed.
Lastly, remove the 2 in b by rooting the other side of the formula.
\(b=\sqrt{c^2-a^2}\)
Step 4: substitute and solve.
\(b=\sqrt{16^2-4^2}\)
\(16×16=256\)
\(4×4=16\)
\(256-16=\sqrt{240}\)
b is 15.49cm
By following and understanding the above example questions, you’ll be able to rearrange the equation and solve any question with ease.
Question 3
Let’s try solving a more complicated question now that we know the basic steps.
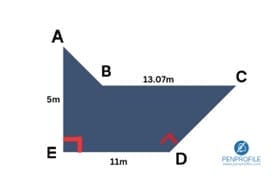
Here we have an irregular polygon and we need to solve for the missing side length: CD.
Step 1: It’s a known rule that whenever you have an irregular shape, the best thing you can do is to break it down into known shapes that you already have the formula for.
We can see that AED is one right angle triangle. Let’s name it triangle 1.
BDC is another right angle triangle that we’ll set as triangle 2.
Triangle 1:
Step 1: identify a, b, c.
c=unknown, b=5m a=11m
Step 2: rearrange the Pythagorean Theorem equation to make c the subject.
\(c=\sqrt{a^2+b^2}\)
Step 3: substitute and solve.
\(a=\sqrt{11^2-5^2}\)
\(11×11=121\)
\(5×5=25\)
\(121-25= \sqrt{96}\)
a is 9.79m
Triangle 2:
Step 1: identify a, b, c.
a is 9.79m as we got from solving triangle 1, c=13.07m, b(CD) is unknown.
Step 2: rearrange the Pythagorean Theorem equation.
\(b=\sqrt{c^2-a^2}\)
Step 3: substitute and solve.
\(b=13.07-9.79\)
\(13.07×13.07= 170.82\)
\(9.79×9.79=95.84\)
\(170.82-95.84=\sqrt{74.98}\)
CD is 8.65m
Question 4
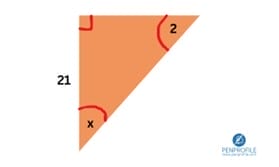
This triangle requires us to find x, but this time it’s for an angle. We won’t be using pythagorean theorem for this but it’s a good practice question for right angle triangles.
The sum of interior angles in a triangle is 180 degrees right?
They already gave us one angle which is 2 degrees. The other angle is going to be 90 degrees because this is a right angled triangle, and even if you can’t tell, the small square indicates it for you.
So, all we have to do now is add 2 and 90 then subtract from 180.
\(90+2=92\)
\(180-92=88\)
x is 88 degrees
Trigonometric functions: Sine, Cosine, and Tangent
Sine (sin), Cosine (cos), and Tangent (tan) are the three out of 6 trigonometric functions, or trig functions for short. These functions are useful with calculations involving right angle triangles and the unit circle.
Sine function
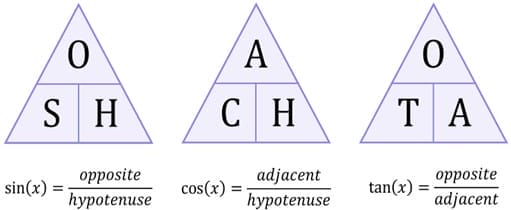
Sine function of an angle is the ratio between the opposite side length to that of the hypotenuse. From that we get the following formula:
Sin(theta)=opposite/hypotenuse. SOH
Cosine function
Cosine function of an angle is the ratio of the length of the adjacent side to the length of the hypotenuse.
Cos(theta)=adjacent/hypotenuse. CAH
Tangent function
The tangent function is the ratio of the length of the opposite side to that of the adjacent side.
Tan(theta)=opposite/adjacent. TOA
Question 1
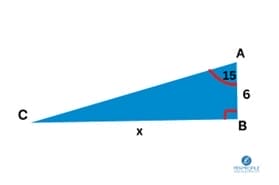
First step in solving the above question is to identify which of SOH CAH TOA we’ll be using.
AC is hypotenuse, BC is opposite, and AB is adjacent.
(Note that all calculations with the calculator involving the trig functions should be in degrees mode.)
We choose which function’s formula we’ll be using based on the information provided.
For example, we can’t use SOH for this question because we don’t have either side lengths of hypotenuse and opposite.
For this question TOA will be the most appropriate
Step 2: substitute and rearrange.
\(\tan(15)=\frac{x}{6}\)
Make x the subject of the formula by multiplying 6 on both sides of the formula to become
\(x=\tan(15)×6\)
When you are putting this value into your calculator ensure that it’s in degrees mode.
Opposite (BA) is 1.6
Even though the question only requires us to solve for x, for the sake of practice let’s solve for AC now that we have BC, using SOH.
\(\sin(15)=\frac{1.6}{x}\)
Make x the subject of the formula by replacing sin(15) with x to become
\(x=\frac{1.6}{\sin(15)}\)
Hypotenuse (AC) is 6.18
Question 2
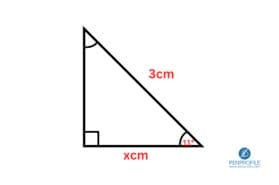
As it’s shown from the picture above, we need the missing length of xcm, which is adjacent. For this question we’ll be using CAH because we have the value of hypotenuse which is 3cm
So by putting everything into formula we get:
\(\cos(11)=\frac{x}{3}\)
Similar to what we did in question one, we’ll simply multiply 3 from both sides of the equation to isolate x and then the formula will become
\(x=\cos(11)×3\)
x is 2.94cm
Question 3
Let’s try solving a question for an unknown angle now.
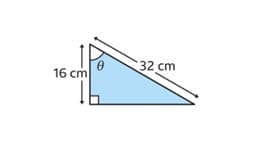
As we see from the picture above, this time we don’t have the value of theta. We can solve these kinds of questions too using the trigonometric functions.
Since we have hypotenuse (32cm) and adjacent (16cm) we can use CAH.
Our formula should be \(\cos(x)=\frac{16}{32}\)
Step 1: simply the formula.
\(\frac{16}{32}\) is 0.5 or ½
Step 2: Rearrange the formula to isolate x.
To make x the subject of the formula we need to move cosine to the other side of the formula. Moving a trigonometric function to the other side of the formula requires us to use its inverse. So:
\(x=\cos^-1(0.5)\)
(You can enter this in your calculator simply by clicking on shift cos)
x is 60 degrees.
Question 4

Recognize this question? Last time we had to solve for x which was 88°. What if x was either adjacent or hypotenuse? In this case we can use the trig functions to find out since we have 1 side length and 1 angle given.
We’ll be solving for the hypotenuse side using sine function.
\(\sin(\theta)=\frac{opp}{hyp}\)
\(\sin(2)=\frac{21}{x}\)
Rearrange the equation by switching x and \(\sin(2)\) to get:
\(x=\frac{21}{\sin(2)}\)
x is 601.72
If you wish, for more practice you can try solving the adjacent side too on your own.
Conclusion
Remember, a right angled triangle always includes a 90 degree angle, as the name implies. To find its lengths, remember that the hypotenuse is the side opposite the right angle and you can determine it using the Pythagorean Theorem. For solving both side lengths and angles, the trigonometric functions Sine, Cosine, and Tangent are what you’ll use and the mnemonic SOH CAH TOA makes it very easy to recall their individual formulas.
This article covers just one aspect of trigonometry, but mastering the basic right-angled triangles and their properties will make solving more complex problems much simpler. Understanding and memorizing these formulas is crucial, because once you do, you’ll be able to manipulate and rearrange them to solve any problem you come across with ease.











